Prim's Algorithm

A greedy algorithm that finds a minimum spanning tree of an undirected weighted graph.

Abstract

Prim’s Algorithm operates by creating an empty tree, adding the edge with the lowest weight that connects a new vertex to the tree, then repeating the process until the tree connects all vertices of the original graph.

Visualisation

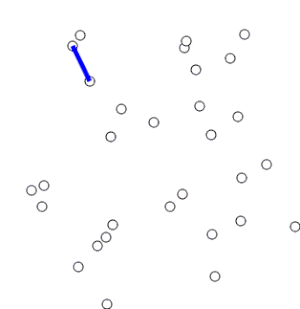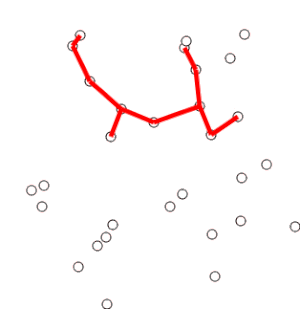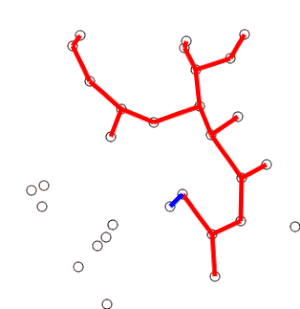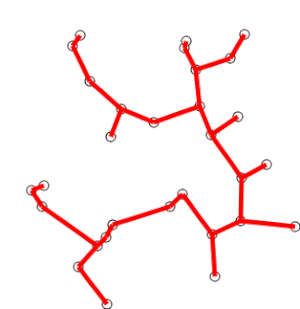
Time complexity

$O(|V{|}^2)$ using adjacency matrix

Implementation

import networkx as nx
 
def prim(graph: nx.Graph) -> nx.Graph:
    tree = nx.Graph()
    tree.add_node(list(graph)[0])
    while len(tree.nodes) < len(graph.nodes):
        edges = []
        for i in graph.edges.data():
            if i[0] in tree.nodes and i[1] in tree.nodes:
                continue
            if i[0] in tree.nodes or i[1] in tree.nodes:
                edges.append(i)
        edges.sort(key=lambda x: x[2]['weight'])
        tree.add_edge(edges[0][0], edges[0][1], weight=edges[0][2]['weight'])
    return tree