Perceptron

An artificial neuron. The simplest artificial neural network architecture, commonly used for binary classification. ¹

Components

Data:

• features: each representing a characteristic of the input data.
• weights: each feature has a weight that determines its influence on an output. These weights are adjusted via training to find their optimal values.
• bias: an adjustable numerical term that is added to the weighted sum before the activation function is applied.
  • This term is independent of the inputs, giving the perceptron more flexibility to fit more complex data.

Functions:

• summation function: function that calculates the weighted sum of its input
• activation function: comparing weighted sum to a threshold to produce a binary output. This is often a Heaviside step function.

The general idea is that different weights will represent the importance of each input, and that the weighted sum should be greater than a threshold value before making a binary decision:

Perceptron Algorithm²

1. Set a threshold value.
2. Multiply all input features with their weights
3. Sum all the results, giving the weighted sum
4. Activate the output

Note will only output binary.

Example

The perceptron decides if we should go to a concert. It will output “Yes” or “No”.

1. Set a threshold value: 1.5
2. Multiply all input features with its weights:
   1. $x_1\times w_1=0.7$
   2. $x_2\times w_2=0$
   3. …
3. Sum the results: for example, $1.6$ (also known as the weighted sum)
4. Activate output: since $1.6>1.5$, return Yes.

Application of obtained weight values

The obtained weight values can be used to form the equation of a line/plane/hyperplane. From the equation

$$\sum _{i=1}^n{w}_i{x}_i-\text{bias}=0$$

For example, for a certain perceptron after training, we obtain the weights $[0.00416,-0.05986]$ and a bias of 0. We can use this to form the equation $0.00416x_1-0.05986x_2=0$. Which becomes a straight line linear classifier for the two regions of the graph, representing for what inputs the perceptron will give what output.

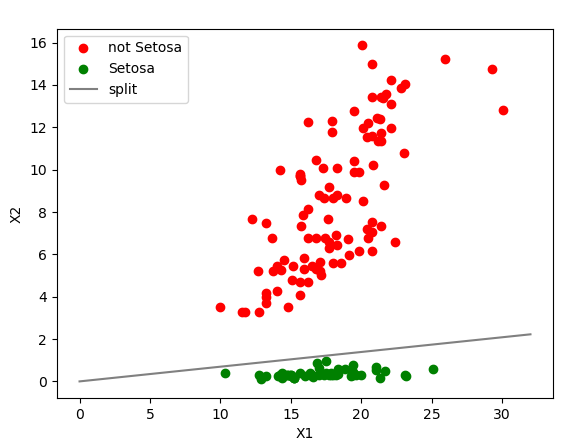
Linear seperation

Limitations

• limited to linearly separable problems
• requires labelled data for training Multi-layer Perceptron overcomes these limitations.

Code

Example of a perceptron

def perceptron(feature_l,weight_l,bias):
    product_list=[feature_l[i]*weight_l[i] for i in range(len(feature_l))]
    result=sum(product_list)+bias
    if result>0:
        return 1
    else:
        return 0

Example of perceptron training

NOTE: This uses a vector module, which can be copied here: Vectors

from ucimlrepo import fetch_ucirepo 
from dataclasses import dataclass
import random
from tqdm import tqdm
 
#This uses a personal vector module, which can be copied from 
# algo25/python/Personal Modules/Vectors
# Use the folling import line, or just copy paste the entire vector class here
from Vector import Vector
 
 
@dataclass         
class AIconfig:
    data_points: list[Vector]=None
    targets:list=None
    weights:Vector=None
    bias:float=None
 
 
def get_data():
    # fetch dataset 
    iris = fetch_ucirepo(id=53) 
    
    # data (as pandas dataframes) 
    iris_features = iris.data.features 
    iris_targets = iris.data.targets 
    
    # get features as seperate lists
    SL=iris_features["sepal length"]
    SW=iris_features["sepal width"]
    PL=iris_features["petal length"]
    PW=iris_features["petal width"]
 
    qty=len(SL)
 
    # obtain features by combining data points
    X1=[SL[i]*SW[i] for i in range(qty)]
    X2=[PL[i]*PW[i] for i in range(qty)]
 
    # obtain lists of targets, or correct answers
    Y=[(1 if fclass == "Iris-setosa" else 0) for fclass in iris_targets["class"]]
 
    # we will store all data points as vectors
    vectorlist=[]
    for i in range(len(X1)):
        vl=[X1[i],X2[i]]
        vectorlist.append(Vector(vl))
 
    return vectorlist,Y
 
 
 
def perceptron(x:Vector,w:Vector,b):
    # simple perceptron
    # DOT PRODUCT OF x and w vectors + bias
    result=x*w+b
    if result>0:
        return 1
    else:
        return 0
 
 
def normal_train(config:AIconfig,nEpoch=1000,learnRate=0.01):
    # training
 
    # gets list of data vectors (x)
    x_l=config.data_points
    
    # finds number of entries, 
    n_entries=len(x_l)
    # finds number of features
    n_features=x_l[0].len()
 
    # populates a weight vector with samed dimensions as data vector
    wl=[0 for _ in range(n_features)]
    config.weights=Vector(wl)
    del wl
 
    targets=config.targets
 
    # initiate a bias
    config.bias=0
    
    for _ in tqdm(range(nEpoch)): #
        
        # iterate through all data items in random order
        i_list=list(range(n_entries))
        random.shuffle(i_list)
        for i in i_list:
            x=x_l[i]
            w=config.weights
            bias=config.bias
 
            res=perceptron(x,w,bias)
            
            # calculates error (if correct, error = 0)
            error=targets[i]-res
 
            # modifies bias and weights
            bias+= error * learnRate
            config.weights+=(x*error)*learnRate
    return config
 
 
def main():
    # extract data
    x_l,targets=get_data()
    
    # initiate config
    config=AIconfig()
    config.data_points=x_l
    config.targets=targets
 
    # initiates training
    normal_train(config)
    
    # outputs the final configuration
    print(f"weights {config.weights}")
    print(f"bias {config.bias}")
 
main()
 

Footnotes

1. https://www.geeksforgeeks.org/machine-learning/what-is-perceptron-the-simplest-artificial-neural-network/ ↩

2. https://www.w3schools.com/ai/ai_perceptrons.asp ↩