Diameter (graph theory)

Warning

This note is not in the study design.

It may contain information that is not relevant to the exam.

Maximum distance between two nodes within a connected graph, where distance between two vertices is defined as the length of the shortest path between the two nodes. It is denoted $diam(G)$, and a deliberate way to confuse things is by calling it the “length of the longest shortest path”.

This is better illustrated by an example.

Definitions and Properties

Define a graph $G=\{N,E\}$. Define $d(a,b)$ to be the distance between the two nodes $a,b$ such that $a,b\in N$. Intuitively:

• $d(a,a)=0$
  • this is the diameter when the graph consists of a single node
• $d(a,b)=1$, where $a,b$ are adjacent
• If $N>2$, then $diam(G)>1$.

Disconnected graphs

Distance is not defined for disconnected graphs, hence some areas say it is infinite¹, undefined, etc - what is emphasised is that that there is no standard definition.

Example

Find the diameter of the following graph:

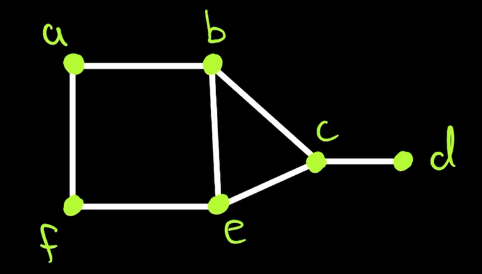
Step 1: List all the distances between each node pair. Exclude the distance to itself (i.e. $d(a,a)$) and the distance between a node and an adjacent node:

• $d(a,e)=2$
• $d(b,d)=2$
• $d(a,c)=2$
• $d(c,f)=2$
• $d(d,e)=2$
• $d(a,d)=3$
• $d(b,f)=2$
• $d(d,f)=3$

Step 2: Find the maximum within these distances. This will be the diameter. Hence, $d(a,d)=d(d,f)=3$ will be the diameter.

Footnotes

1. https://mathworld.wolfram.com/GraphDiameter.html ↩