Complexity Classes

Complexity Classes are sets of problems that are related in complexity. The complexity classes used in Algorithmics are for decision problems (given an input, the algorithm returns yes or no depending on some statement).

Visualisation

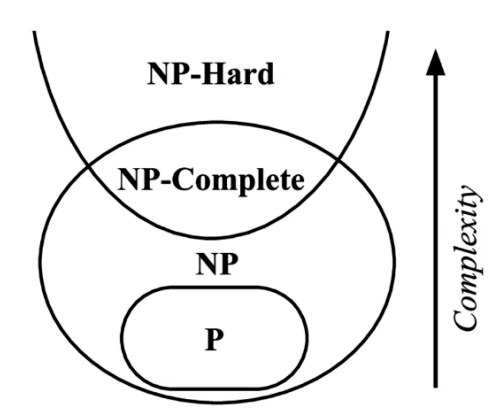
P (Polynomial Time)

P contains all decision problems that are tractable - that is, the problem has a solution that can be found in polynomial time. Polynomial-Time problems are deterministic algorithms. The class P is a subset of class NP.

$$T(n)=O(n^k),k\in {\mathbb{Z}}^{+}\cup \{0\}$$

$O(2^n),O(n!),O(n^n)$ do not count as polynomial time.

NP (Non-deterministic Polynomial Time)

NP contains all decision problems that are intractable. Criteria: cannot be solved in P time, but can be checked and verified in P time That is, the problem either has solutions already found and are verifiable in polynomial time, or can be solved in non-deterministic polynomial time (by random chance). These problems can be solved on a non-deterministic Turing machine. An unsolved question is whether P=NP however it is generally believed that P≠NP.

NP-Complete

The set of all decision problems $X$ in NP for which it is possible to reduce any other NP problem $Y$ to $X$ in polynomial time. This means we can solve $Y$ quickly if we know how to solve $X$ quickly. This also means any NP-Complete problem can be reduced to any other NP-Complete problem. If any one NP-Complete problem can be solved in polynomial time, then every problem in NP can also be solved in polynomial time, meaning P expands to contain all of old NP.

Examples

• 0-1 Knapsack Problem (Decision)
• Graph Coloring Problem
• Travelling Salesman Problem (TSP) (Decision)/ finding Hamiltonian path

NP-Hard

NP-Hard contains all problems in NP-complete. NP-Hard problems are at least as hard as the NP-complete problems. NP-Hard problems do not have to be in NP, as they do not have to be decision problems. If problem $X$ is NP-Hard, there is a NP-complete problem $Y$ such that $Y$ is reducible to $X$ in polynomial time.

The segment of NP-Hard that excludes NP-Hard, is not verifiable in polynomial time as it does not lie within NP.

A reduction is a method of solving a problem by converting that problem into an instance of a second problem which has a known solution, and using that solution to solve the first problem. If any NP-hard problem can be solved in polynomial time, all NP problems can be solved in polynomial time. Some NP-hard problems are not even verifiable in polynomial time.

Examples

• Halting Problem
• 0-1 Knapsack Problem (Optimal)
• Travelling Salesman Problem (TSP) (Optimal)/ finding Hamiltonian path
• Any NP-complete problem is NP-hard.