Big-O Analysis

Abstract

Big-O is a way to describe the time or space complexity of algorithms. It expresses an upper bound of an algorithm’s time or space complexity, a measure of the “worst case scenario”.

Why (application/feasibility)

• allows programmers to compare different algorithms and choose the most efficient one
• helps in understanding scalability of algorithms and predicting how they will perform as input size grows
• enables developers to optimise code and improve performance

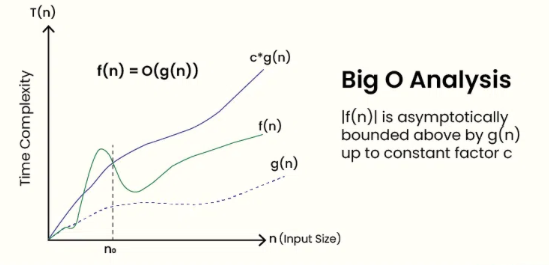
Formal Mathematical Definition

Given two functions $f(n)$ and $g(n)$ We say that $f(n)=O(g(n))$ if there exists constants $c>0$ and $n_0\ge 0$ such that $c\times |g(n)|\ge |f(n)|$, for all $n\ge n_0$. In other words, $f(n)$ grows no faster than $c\times g(n).$

$$[\exists c>0,\exists n_0\ge 0\text{ s.t }(\forall n\ge n_0,c\cdot |g(n)|\ge |f(n)|\left)\right]⟹f(n)=O(g(n))$$

How to find Big-O

• ignore lower order terms, consider highest order term (e.g. term with highest power)
• ignore constant (coefficient) associated with highest order term
• see Other Examples of Big-O for simple/difficult examples

Why we concatenate log terms

Say we had a program of Big-O of $lo{g}_{3}n$ Let $c$ be a constant $lo{g}_{3}n=\frac{lo{g}_{c}n}{lo{g}_{c}3}$ As $\frac{1}{lo{g}_{c}3}$ is a constant coefficient, it can be taken out and ignored for Big-O notation. As such, the Big-O notation of any log term can be converted to have any base term. $O(lo{g}_{3}n)=O(lo{g}_{c}n)$ Thus the base term simply does not matter and can be ignored, and written as $O(\log n)$

Properties

• reflexivity: for any function $f(n)$, $f(n)=O(f(n))$

• transitivity: if $f(n)=O(g(n))$ and $g(n)=O(h(n))$, then $f(n)=O(h(n))$

• nonzero constant factor: if $f(n)=O(g(n))$, then $k\times f(n)=O(g(n))$

  • constant multiplicative coefficients do not affect Big-O term

• sum: if $f(n)=O(g(n))$ and $h(n)=O(k(n))$, then $f(n)+h(n)=O(max(g(n),k(n)))$.

  • In other words, when combining complexities only the largest term dominates

• product rule: if $f(n)=O(g(n))$ and $h(n)=O(k(n))$, then $f(n)h(n)=O(g(n)k(n))$

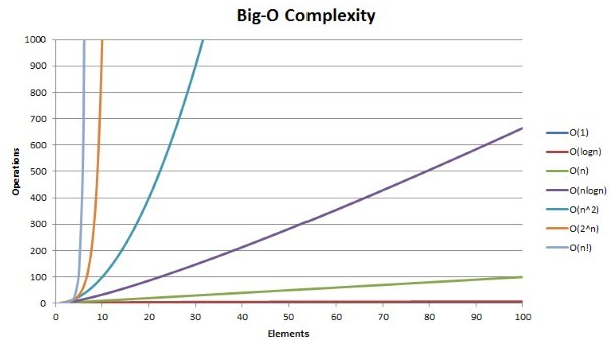
Relative size

$$O(\log n)\le O(n)\le O(n\log n)\le O(n^2)\le O(n^3)\le O(2^n)\le O(n!)$$

Amortized time

Amortized time instead focuses on the average time to run, rather than the worst-case performance of the algorithm. Amortized time is determined by dividing the total running time, by the number of operations and is expressed in Big-O notation. For example, if an algorithm run an arbitrary $n$ number of times runs in $O(n)$, then the amortized time is $O(n)/n=O(1)$.