An iterative heuristic search algorithm designed to solve problems where the goal is to find an optimal solution moving from the current state to a better neighbouring state, according to a heuristic function (or evaluation function)1
Steps
- Initial state: start with a random solution
- Neighbouring states: identify neighbouring states by making small adjustments (mutations)
- Move to neighbour: if one of the neighbouring states offers a better solution according to the heuristic function, move to this new state
- Termination: repeat this process until no neighbouring state is better than the current one. We have reached a local maximum or minimum. The steps reflect the algorithm’s greedy approach.
Termination
Hill climbing will approach a locally optimal solution (any small changes will be worse), which may not be the globally optimal solution. For details, see the diagram below. This can partially be resolved through the use of simulated annealing.
State space diagram
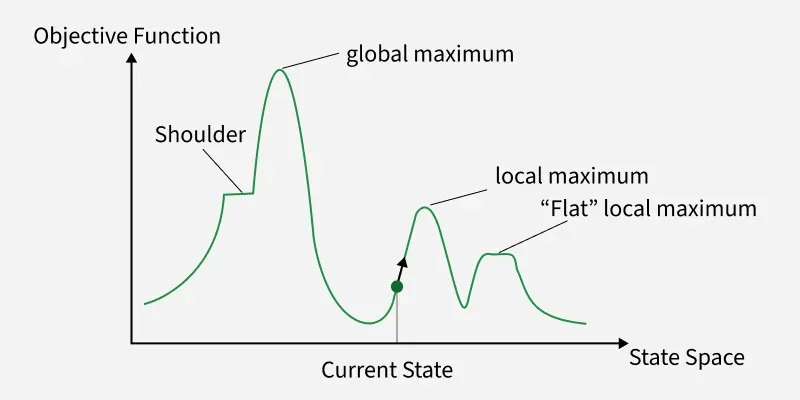 From this diagram, note key regions:
From this diagram, note key regions:
- local maximum: a state better than its neighbours, but not the best overall. However, the algorithm will terminate here.
- global maximum: optimal solution the algorithm seeks.
- flat local maximum: flat region where neighbouring states have the same heuristic function, making it difficult for the algorithm to decide on the next move.