Transitive Closure

The transitive closure of a graph refers to whether node A can be reached from node B for all node pairs (A, B).

Graph state

When described as a graph, it is a graph which contains an edge between A and B whenever there is a directed path from A to B. In other words, every path in the graph is directly added as an additional edge.¹

Matrix state

When described as a matrix, it is a $|N|\times |N|$ matrix $T$, where $T_{ij}$ reflects whether node $i$ can reach node $j$. The rows represents the source node (‘from’) and columns represent the target node (‘to’). 0 means not reachable and 1 means reachable:

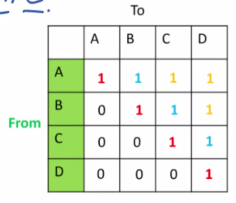
Properties:

• Unlike adjacency matrix, the value of the pair ($A$, $A$) where A is any node within the graph is always 1, as there exists a path from a node to itself, although controversy exists.²
• For a completed undirected graph, all cells would be 1, as all nodes would be reachable from any other node. As such transitive closure is only applied to directed graphs.

Footnotes

1. Alexandria Repo, p134 ↩

2. There is debate on if the main diagonal should be 0 or 1. The prevalent argument is that a node should be reachable from itself as you are already there, therefore the main diagonal should be 1 going by this argument. ↩