Multi-layer perceptron (MLP) is a modern neutral network architecture consisting of fully connected perceptrons with nonlinear activation functions, organised in layers. It is notable for being able to distinguish data that is not linearly separable.
Multi-layer
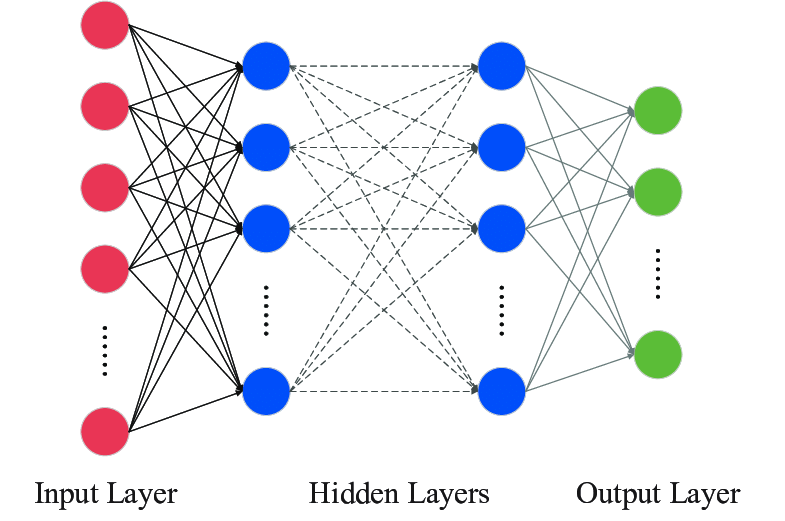
A MLP are composed of perceptrons arranged in layers:
- Input layer: each perceptron corresponds to an input feature
- Hidden layer(s): can have any number of hidden layers containing any number of perceptrons. These layers process the information received from the input layer.
- Output layer: generates the final prediction or result. If there are multiple outputs, the layer will have a corresponding number of perceptrons.
Visualisation
Important: note that MLPs are fully connected in a way that every node in one layer connects to every node in the next layer.
It is a -partide complete graph.
Feedforward
MLPs are feedforward, meaning that information flows in a single direction, i.e. from the input layer to the hidden layer to the output layer without loops or feedback.
Evaluation
Evaluation of outputs are done via forward propagation, where the data flows from the input layer to the output layers, passing through any hidden layers.
Each hidden layer processes inputs as follows:
- compute weighted sum of inputs as well as adding any bias
- weighted sum is passed through an activation function which is often non-linear. Common activation functions include sigmoid, ReLU, or tanh.
- output to another hidden layer or the output layer
Loss function
When the network generates an output, we should calculate the loss using a loss function. In supervised learning, this compares the predicted output to the actual label.
The functions are not covered in the study design, but common functions include mean squared error or binary cross-entropy.
Training
The goal of training an MLP is to minimise the loss function by adjusting the networks weights and biases. This is done through back-propagation:
- gradients of loss function with respect to each weight and bias is calculated
- error is propagated back through the MLP
- network updates the weight and biases by moving in the opposite direction of the gradient to reduce the loss