Adjacency matrix

The adjacency matrix $A$ of a graph is a $n\times n$ matrix in which, for example, the entry in row $C$ and column $F$ ($A_{c,f}$) is the number of edges joining nodes C and F.

Difference to Incidence Matrices

The adjacency matrix represents relations between node-node pairs. An incidence matrix represents relations between node-vertex pairs.

Loops

A loop is a single edge connecting a node to itself. If node A has a loop, then its corresponding entry on the adjacency matrix $M_{a,a}$ will have value 1, as a loop is considered 1 edge.

Example

An undirected graph on the left and the adjacency matrix on the right: 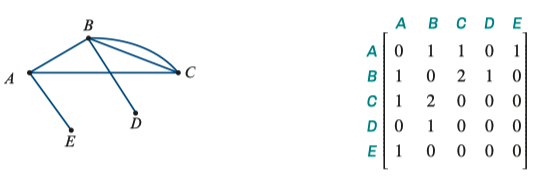A directed graph example:

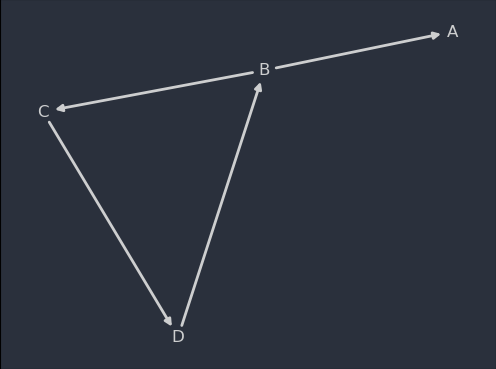
		Target
		A	B	C	D
Source	A	0	0	0	0
	B	1	0	1	0
	C	0	0	0	1
	D	0	1	0	0
Note how the adjacency matrix is no longer symmetric, compared to the undirected graph example.