Warshall's Transitive Closure Algorithm

Abstract

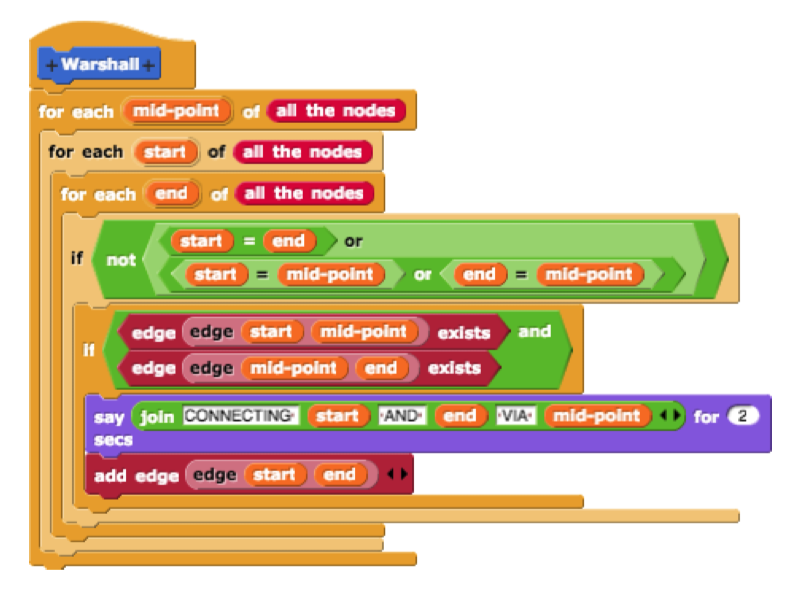
Recall that within transitive closure, a graph representation can be created by adding each directed path between every pair of nodes within the graph. A more direct way is to simply iterate the process of concatenating two edges (either already in the graph or inserted earlier) by iterating all the possible combinations of a start node, end node, and a middle node at which the two edges connect. In other words, we look for a combination of edges $(A,C)$ and $(C,B)$ and insert a new edge $(A,B)$ whenever we find such a pair. This is Warshall’s transitive closure algorithm.¹

Pseudocode

Algorithm Warshall

input: graph G
output: transitive closure of G

FOR EACH middle in G.nodes
	FOR EACH start in G.nodes
		FOR EACH end in G.nodes
			IF NOT edgeExists(G, start, end) THEN
				IF edgeExists(G, start, mid) AND 
				edgeExists(G, mid, end) THEN
					addEdge(G, start, end)
				END IF
			END IF
		END FOR EACH
	END FOR EACH
END FOR EACH

RETURN G

Edgy

Python

  
 
def transitive_closure(graph:nx.DiGraph):
 
    reachable = {}
    nodes = list(graph.nodes)
    # initalise 2 key dict with unreachable 0
    for node1 in nodes:
        reachable[node1]={}
        for node2 in nodes:
            reachable[node1][node2] = 0
    # set nodes to them selves as reachable
    for node in nodes:
        reachable[node][node]=1
    # set reachable for every given edge
    # diffrence is for digraph it only populates in direction of one
    for edge in graph.edges.data():
            node1, node2, pdict = edge
            reachable[node1][node2]=1
 
    # up to here reachable is an adjacency matric as a dualkey dictionary
    # print(reachable)
    
    # important for intermedate node loop to be on outside (?) might be absolutely nessicary for relaxation
    for intermediaryNode in nodes:
        for nodeI in nodes:
            for nodeJ in nodes:
                # if unreachable
                if reachable[nodeI][nodeJ] != 1:
                    if reachable[nodeI][intermediaryNode] and reachable[intermediaryNode][nodeJ]:
                        # sees if using intermediaryNode between nodeI to nodeJ is reachable
                        reachable[nodeI][nodeJ] = 1
    return reachable

Correctness

We use proof by induction to prove the algorithm’s correctness. Given the basis of the outer loop, we assume that we iterate through the nodes in some ordered arbitrary sequence from $1\dots |N|$.

It is easy to see that the $k$-th iteration of the outer loop establishes all paths that only uses nodes $1\dots k$ as intermediate nodes.

At the $(k+1)$-st iteration all possible paths from $A$ to $B$ that only use $1\dots k$ as intermediate nodes have already been established earlier by induction. A new cycle-free path using $(k+1)$ can only arise if there is an edge from $A$ to $(k+1)$ and one from $(k+1)$ to $B$ that can be joined with $(k+1)$ being the intermediate. Each of these edges is either an original edge or arose from a path that only uses nodes $1\dots k$. By inserting edges from $A$ to $B$ for all such cases the $k$-th iteration establishes all possible paths that only uses nodes $1\dots k$ as intermediate nodes. Thus the algorithm correctly generates the transitive closure after $|N|$ iterations out of the outer loop.

Footnotes

1. Alexandria Repo, p134 ↩